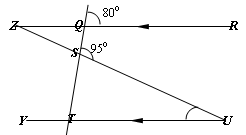$\begin{align}  & \text{You need to do some extending of the lines to solve this question}.\text{ Let get started}.~~ \\ & \text{Produce }QS\text{ to meet line}\mathbf{UT},\text{ also produce }\mathbf{SU}\text{ to meet }\mathbf{QR}~ \\ & \angle AQR=\angle ATU={{80}^{\circ }}\text{      }\!\!\{\!\!\text{ corresponding angle }\!\!\}\!\!\text{ } \\ & \angle QSU+\angle UST={{180}^{\circ }}\text{      }\!\!\{\!\!\text{ Sum of angles on a straight line }\!\!\}\!\!\text{ } \\ & \text{9}{{\text{5}}^{\circ }}+\angle UST={{180}^{\circ }} \\ & \angle UST={{85}^{\circ }} \\ & \text{Consider }\Delta STU \\ & \angle STU+\angle TUS+\angle UST={{180}^{\circ }}\text{  }\!\!\{\!\!\text{ sum of angles in a }\Delta \text{ }\!\!\}\!\!\text{ } \\ & {{80}^{\circ }}+{{85}^{\circ }}+\angle TUS={{180}^{\circ }} \\ & \angle TUS=x={{15}^{\circ }} \\\end{align}$