Jambmaths question:
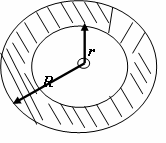 In the diagram above are two concentric circles of radii r and R respectively with centre O. If $r=\tfrac{2}{5}R$, express the area of the shaded portion in term of $\pi $and R
In the diagram above are two concentric circles of radii r and R respectively with centre O. If $r=\tfrac{2}{5}R$, express the area of the shaded portion in term of $\pi $and R
Option A:
$\tfrac{21}{25}\pi {{R}^{2}}$
Option B:
$\tfrac{9}{25}\pi {{R}^{2}}$
Option C:
$\tfrac{21}{23}\pi {{R}^{2}}$
Option D:
$\tfrac{5}{9}\pi {{R}^{2}}$
Jamb Maths Solution:
$\begin{align} & \text{Area of the circle with radius}r=\pi {{r}^{2}}=\pi {{\left( \tfrac{2}{5}R \right)}^{2}}=\tfrac{4}{25}\pi {{R}^{2}} \\ & \text{Area of the circle with radius}R=\pi {{R}^{2}} \\ & \text{Area of the shaded portion}=\pi {{R}^{2}}-\tfrac{4}{25}\pi {{R}^{2}} \\ & =\pi {{R}^{2}}\left[ 1-\tfrac{4}{25} \right] \\ & =\pi {{R}^{2}}(\tfrac{21}{25}) \\ & =\tfrac{21}{25}\pi {{R}^{2}} \end{align}$
Jamb Maths Topic:
Year of Exam:
