Jambmaths question:
Find the locus of a particle which moves in the first quadrant so that it is equidistant from the line x = 0 and y = 0 (where k is a constant)
Option A:
$x+y=0$
Option B:
$x-y=0$
Option C:
$x-y-k=0$
Option D:
$x+y+k=0$
Jamb Maths Solution:
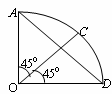
Answer Option B
The locus of the particle is the line passing through the origin (which make k = 0) and is the bisector of AO and OD (i.e line OC will bisect $\angle AOD$) which makes $\angle COD={{45}^{\circ }}$
The slope is $m=\tan \theta =\tan {{45}^{\circ }}=1$
Using one point slope equation $(x,y)=(0,0)$
$(y-{{y}_{1}})=m(x-{{x}_{1}})$
$y-0=1(x-0)$
$y=x$
$x-y=0$
Jamb Maths Topic:
Year of Exam:
