Jambmaths question:
An equilateral triangle of sides $\sqrt{3}$is inscribed in a circle. Find the radius of the circle.
Option A:
$\tfrac{2}{3}$cm
Option B:
1cm
Option C:
2cm
Option D:
3cm
Jamb Maths Solution:
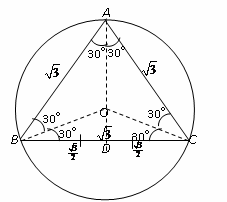 $\begin{align} & AD=\sqrt{3}\sin {{60}^{o}}=\sqrt{3}\times \frac{\sqrt{3}}{2}=\frac{3}{2} \\ & \angle OBD={{30}^{o}}\text{ }\!\!\{\!\!\text{ Angular bisector of }\angle ABC\} \\ & \frac{OD}{BD}=\tan {{30}^{o}} \\ & OD=BD\tan {{30}^{o}} \\ & OD=\frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{3}}=\frac{1}{2} \\ & OA=AD-DO=\frac{3}{2}-\frac{1}{2}=\frac{2}{2}=1 \\ & AO=1cm \\\end{align}$
$\begin{align} & AD=\sqrt{3}\sin {{60}^{o}}=\sqrt{3}\times \frac{\sqrt{3}}{2}=\frac{3}{2} \\ & \angle OBD={{30}^{o}}\text{ }\!\!\{\!\!\text{ Angular bisector of }\angle ABC\} \\ & \frac{OD}{BD}=\tan {{30}^{o}} \\ & OD=BD\tan {{30}^{o}} \\ & OD=\frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{3}}=\frac{1}{2} \\ & OA=AD-DO=\frac{3}{2}-\frac{1}{2}=\frac{2}{2}=1 \\ & AO=1cm \\\end{align}$
Jamb Maths Topic:
Year of Exam:
